Puzzling Rhombic Dodecahedron

What is this ?

I have the chance to own a “scorpius slider spider puzzle”, a piece of wood art offered to me more than 30 years ago as I was a child.
I wanted to try a reproduction to publish in Shadertoy.

preview

I learnt reading Philippe Cichon’s blog that it’s a rare puzzle, very few makers exists !

This video of Philippe Cichon shows how to mount and unmout it (in French)
Le Scorpius on Youtube

About The Puzzling World of Polyhedral Dissections

With Philippe Cichon’s blog, I discovered a puzzling book available online for free !

The Stewart Coffin’s book The Puzzling World of Polyhedral Dissections has been made available on the Internet by John Rausch

The Puzzling World of Polyhedral Dissections was obviously not written by Stewart to get rich. Anyone who produces such works does it as a labor of love for a subject that is very dear to them. As puzzle collectors, we owe Stewart a huge debt of gratitude for sharing with us his knowledge about the mathematics, aesthetics and philosophy of geometric puzzles. If you enjoy it as much as I do, drop Stewart a line and thank him for his unselfish gesture.

So, during a recent visit with Stewart, I asked him what he thought about publishing it on the Internet. I hope you are as happy as I am that he said, “go for it!”

John Rausch Oregonia, Ohio 1998

How it looks after modeling it with Shadertoy

I challenged myself to model this puzzle on Shadertoy, and here is the result after many hours of drawing on paper and testing.

The rendering is very slow, each of the 24 pieces are evaluated for distance estimation.

Draw the pieces of the puzzle

I first tried to reproduce the plans kindly put online by Philippe Cichon.

I quickly realized that there was a problem with an essential angle allowing the assembly of the puzzle.

Refering to the article on Philippe Cichon’s blog (French), this angle is 70 degres, but it is only an approximation.

The explanation is in the design of this puzzle, mentioned in the Stewart Coffin’s book The Puzzling World of Polyhedral Dissections. This sentence of the book gives somes clues.

The rhombic dodecahedron can be totally enclosed by a symmetrical cluster of 12 sticks having equilateral-triangular cross-section.

As the pieces are placed on the faces or an inner rhombic dodecahedron, this angle is formed when 2 pieces on 2 different faces overlap.

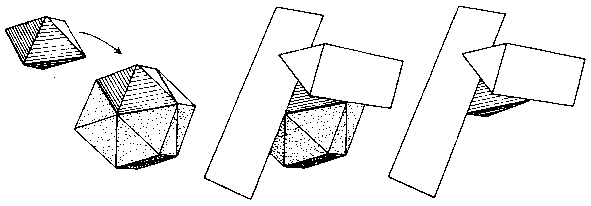
preview

The first piece is oriented along one border of the rhombus, the second aligned with the other.

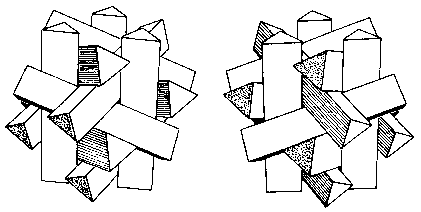
preview

Illustration using Shadertoy

Exercice to verify the acute angle

The Wikipedia page about the Rhombic dodecahedron mention that $\arccos(\frac{1}{3})$ is the acute angles on each face.

This angle is a key to calculate the relative postition of the holes and pins of the puzzle.

The long face-diagonal length is exactly √2 times the short face-diagonal length, thus.

preview

$ \tan(\frac{\theta}{2}) = \frac{1}{\sqrt2} \
\theta = 2\times\arctan{\frac{1}{\sqrt2}} $

Wikipedia gives a different expression for it : $\arccos(\frac{1}{3})$, it appears that this is the same value.

Using al-Kashi (Pythagore generalized)

$a^2=b^2+c^2-2b\cdot c\cos(\theta).$
$a=2, b=c=\sqrt3$
$\cos(\theta) = \frac{4-3}{3}$
$\cos(\theta) = 1/3$

This can be also be verified using the half arc formula.

Fonction circulaire réciproque - Wikipedia
Tangent half-angle formula - Wikipedia

\[\arccos(x) = 2\times\arctan(\frac{\sqrt{1-x^2}}{1+x})\]

Applied with $x = \frac{1}{3}$

\[\arccos(\frac{1}{3}) = 2\times\arctan(\frac{\sqrt{\frac{8}{9}}}{\frac{4}{3}}) = 2\times\arctan(\frac{\sqrt{2}\times\frac{2}{3}}{\frac{4}{3}}) = 2\times\arctan(\frac{1}{\sqrt{2}})\]

Description of the pieces

Details of the front view of one of the 24 puzzle’s pieces.
These are equilateral-triangular cross-section, cutted in half.

preview

Developped view, 70,5° is the approxiated value of $\arccos(\frac{1}{3})$

preview

Notes about calculations (messy, hope I will be able to rework it some day)

Using some trigonometry

preview

symbol	value	explanation	calculation
trnc	10%	pencentage of trucation of the top of the piece.	free choosen value, adds complexity in the calculations compared to a simple triangular shape. My own version has no truncation.
k	1,732	square root of 3, Pythagorean theorem applied to the height of an half equilateral triangle.	sqrt(3)
f1	15.0 mm	width of face 1	unit for calculations
f2	27.0 mm	width of face 2	2 * f1 * (1-trnc)
f3	1.5 mm	width of face 3	f1 * trnc
f4	23.4 mm	width of face 3	f1 * k * (1-trnc)

symbol	value	explanation	calculation
rdan	70,5°	the acute angles on each face of the rhombic dodecahedron	acos(1/3)
d1	15,91 mm	half side of the Rhombic face.	f1/sin(rdan)
d2	14,32 mm	Corrected (because of truncation) half side of the Rhombic face.	d1 * (1-trnc) or (1-trnc) * f1/sin(rdan)
slope	35,36%	slope of the bended lines in comparison with an horizontal line. Usefull to compute the point coordonates.	1/tan(rda) or 1/(3 * sin(rda))
A.x	15,00 mm	x Coordinate of A from the rhombus center. This point can be visualized as the bottom point of the 6 “craters” of the puzzle !	f1
A.y	21,21 mm	y Coordinate of A from the rhombus center.	d1+f1 * slope or f1 * (4/3)/sin(rdan)
B.x	-7,50 mm	x Coordinate (relative to A) of B, pivot point on face 1.	-f1/2
B.y	11,67 mm	y Coordinate (relative to A) of B, pivot point on face 1.	d2-f1 * slope/2
C.x	13,5 mm	x Coordinate (relative to A) of C, pivot point on face 2.	f2/2
C.y	-3,18 mm	y Coordinate (relative to A) of C, pivot point on face 2.	(f2 * slope-d1)/2

Details of the calculations using Desmos.

References

PuzzlingWorld By Stewart T. Coffin
Rhombic dodecahedron SDF from yx on Shadertoy

My illustrations on Shadertoy

Adam Savage’s One Day Builds: Rhombic Dodecahedron with Matt Parker!
My illustration using p5js and loading an OBJ mesh file created using Autodesk fusion 360 (free for personal use).

Reference : The Coding Train : 18.7: Loading OBJ Model - WebGL and p5.js Tutorial

Math formulas and GitHub pages

I used the method described in this page to render Latex mathematical expressions in GitHub pages.
Please note that you just need to copy from the Theme repository and customize the default.html file in the _layouts folder and add the below lines at the end. Fortunately there is no need to duplicate the whole Theme repository in your GitHub pages repository.

<script>
MathJax = {
  tex: {
    inlineMath: [['$', '$'], ['\\(', '\\)']]
  },
  svg: {
    fontCache: 'global'
  }
};
</script>
<script type="text/javascript" id="MathJax-script" async
  src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js">
</script>